深度学习专业深度学习与神经网络简介

随着ChatGPT的爆发以及近期大规模模型竞赛的爆发，AI行业逐渐走进了大众的视野。作为一个喜欢鼓捣各种技术的爱好者，我自然希望了解其中涉及到的一些原理。但如果我想更好地理解人工智能领域的知识，我认为从深度学习入手并没有错。之前学过吴恩达-教授机器学习课程，这次我又选了一门他的特色科目。专攻深度学习，学习深度学习。本文主要以第一门课程为参考，尝试以通俗的方式向大家介绍深度学习。

1。神经网络简介及基本概念

神经网络是模拟人脑神经网络进行分布式并行信息处理的算法模型。它由大量互连的节点（或神经元）组成。每个神经元都可以使用简单的信号处理函数处理输入信号，并将处理结果传递给后续神经元。这些计算的目的是最小化网络的预测误差，这是通过不断调整网络中的参数（即神经元之间的连接权重）来实现的。如图是几种常见神经网络的示例，包括标准神经网络、卷积神经网络（CNN）和循环神经网络（RNN）。 常见神经网络

为了更好地深入研究这个话题，我们首先介绍神经网络的几个关键概念。

1.1 损失函数

损失函数衡量我们模型对一个样本的预测结果与实际结果之间的差异。例如，对于二分类问题，常用的损失函数是交叉熵损失。假设我们的模型预测样本属于正类的概率为，样本的真实标签为（为0或1），那么交叉熵损失函数可以定义为：

该函数表示真实标签与预测概率之间的差异：当真实标签接近预测概率时，损失接近于零；当真实分数与预测概率相差甚远时，损失就会变得非常大。

1.2 成本函数

虽然损失函数衡量的是单个样本的预测误差，但我们通常衡量的是整个训练集的预测误差，这就需要用到成本函数。成本函数是样本损失函数所有值的平均值。对于交叉熵损失函数，假设我们有 个样本，则成本函数 可以定义为：

在神经网络中，我们的目标是找到最好的 和 ，使得成本函数最小化，这通常通过梯度下降等优化算法来实现。

1.3 梯度下降

为了找到最小化成本函数的参数，我们通常使用称为梯度下降的优化算法。在每次迭代中，我们首先计算成本函数相对于每个参数的梯度，然后更新参数：

其中 是学习率（learningrate） 控制更新步长尺寸。 和是成本函数相对于参数和的偏导数，表示当前位置的变化程度的参数。

通过多次迭代，我们可以逐渐接近最小化成本函数的参数，从而优化我们的模型。

1.3.1 批量梯度下降、随机梯度下降和小批量梯度下降（Stochastic Gradient Descent）和小批量梯度下降（Mini-batch Gradient Descent）。

• 批量梯度下降：在每次迭代中，我们使用整个数据集来计算梯度并更新参数。该方法的优点是方向准确，不易陷入局部最优。但缺点是当数据集较大时，每次迭代的计算量会很大，计算速度会很慢。
• 随机梯度下降：在每次迭代中，我们仅使用一个样本来计算梯度并更新参数。该方法的优点是计算速度高，能够快速收敛，但缺点是由于一次只使用一个样本，更新方向波动较大，可能会错过全局最优。
• 小批量梯度下降：这是上述两种方法的折衷方案，使用小批量的样本来计算梯度并更新每次迭代的参数。该方法结合了批量梯度下降和随机梯度下降的优点，既能保证一定的计算速度，又能保证梯度方向的准确性。这是实际应用中最常用的方法。

1.3.2 梯度下降面临的挑战及对策

虽然梯度下降是一个强大的优化工具，但在实践中我们可能会遇到一些挑战：

• 局部最优：梯度下降有可能会陷入局部最优，并且未能找到全局最优解。解决此问题的常见策略是使用随机初始化或使用更复杂的优化策略，例如自举梯度下降，Adam 等人。
• 消失和爆炸梯度：在深度神经网络中，梯度在反向传播过程中可能变得非常小（消失梯度）或非常大（爆炸梯度）。解决这个问题的策略包括使用ReLU等不饱和激活函数，或者使用批量归一化、残差结构等。
• 选择合适的学习率：学习率太大，梯度下降可能不收敛；如果学习率太低，梯度下降可能会非常慢。解决此问题的策略包括学习率衰减或使用 Adam 等自适应学习率优化器。

通过对梯度下降的深入理解，我们可以更好地理解神经网络的训练过程，并可以更好地控制和优化训练过程。

1.4 神经网络中的数学符号

神经网络包含许多数学符号。让我们来了解一些最基本的符号。

• ：表示第个样本的特征向量。
• ：代表真实标记。
• ：表示想要的图案标记。
• ：表示第层的权重矩阵。
• ：表示第层的偏置向量。
• ：表示第层的激活值。
• ：表示第层的线性输出，即。
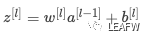• ：表示样本数。
• ：第层的节点数。
• ：表示输入层的节点数，即特征数。
• ：表示输出层的节点数，即标签类别的数量。
  其实主要要记住三点：
• 右上角的方括号代表层
• 右上角的圆括号代表示例 数字在较低的右角代表神经元

这些符号构成了神经网络的基本语言。通过理解它们，您将能够理解神经网络如何工作以及如何以数学方式实现它们。如果您现在不记得这些公式也没关系。当你在文章中看到它们时，你可以再次检查它们。

2。激活函数

激活函数在神经网络中发挥着重要作用。它将非线性因素添加到神经网络中，使其能够适应更复杂的模型。在本章中，我们将详细介绍几种常见的激活函数及其属性。

2.1 Sigmoid函数

Sigmoid函数是神经网络中最早使用的激活函数。表达式为：

其特点是其结果在(0, 1)之间，因此可以理解为概率。另外，当z趋近正无穷大时，a趋近1，当z趋近负无穷大时，a趋近0，它经常被用作二元分类问题中输出层的激活函数，将输出解释为概率。 sigmoid

Sigmoid函数常用于分类算法逻辑回归。该算法主要用于二分类问题。其目标是找到一种可以根据输入特征预测事件概率的模型。该预测概率是逻辑回归模型的结果。

但是，当sigmoid函数的输入值的绝对值较大时，函数的梯度接近0，会导致梯度消失，导致神经网络的训练变得困难。此外，sigmoid 函数的输出不以 0 为中心，这可能会导致训练过程中收敛速度变慢。

2.2 Tanh函数

Tanh函数可以理解为Sigmoid函数的扩展，将输入压缩到(-1,1)。 Tanh函数的表达式为：

由于Tanh函数的结果以0为中心，因此在实际应用中Tanh函数通常比sigmoid函数表现得更好。 tanh

然而，Tanh函数仍然存在梯度消失的问题。当输入值的绝对值较大时，函数的梯度接近于0。

2.3 ReLU函数（修正线性单元、线性整流函数、修正线性单元）

ReLU函数是目前比较常用的函数在神经网络中使用激活函数。 ReLU函数的表达式为：

ReLU函数在x>0时保持输入不变，在x0时ReLU函数的梯度为1，当x